The Thermal Data
A total of 6 tests were conducted at 1.0 GPM with fan speeds of 750 rpm, 1300 rpm and 1850 rpm being run in ‘Push Only’ and ‘Push/Pull’. All inclusive this testing takes between 40 – 50 hours of logging time (plus processing the data) to get the results that are presented.
Below is the final data results gathered from at least 5 data logging runs at the flow rate and fan rpm combination. The most stable 15 minute period from each logging run was used and then averaged with the other runs to obtain the data for the table below. A total of 16 temperature sensors are used in the thermal test chamber (8 air in, 2 air out, 3 water in, 3 water out). Each sensor takes a reading every second and is logged via a CrystalFontz unit.
The data in the table below is the averaged results of the logging runs which has then been used to create all the plots and tables there-after.
The performance metric of critical importance is the delta between the warm coolant temperature in and the cool ambient air temperature going into the radiator. Given that the system is well insulated and in equilibrium and we know the heat input to the system then we can also calculate a very important number. That number is the amount of power required to raise the coolant temperature by set amount. That amount is typically 1C or 10C. The latter is a more useful reference point.
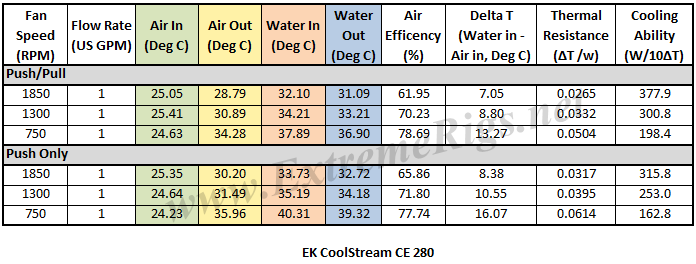
Let’s take a look at the Delta T results from the tests. Note that the extrapolation of the curve is much more sensitive to error than in the tested range.
I was not too concerned about the actual delta numbers but instead the trend pattern. As we should expect, the deltas come down as the fan speed is increased. The less significant temperature drop from 1300 to 1850 rpm indicates the bulk of this radiators performance potential can be achieved with medium fan speeds.
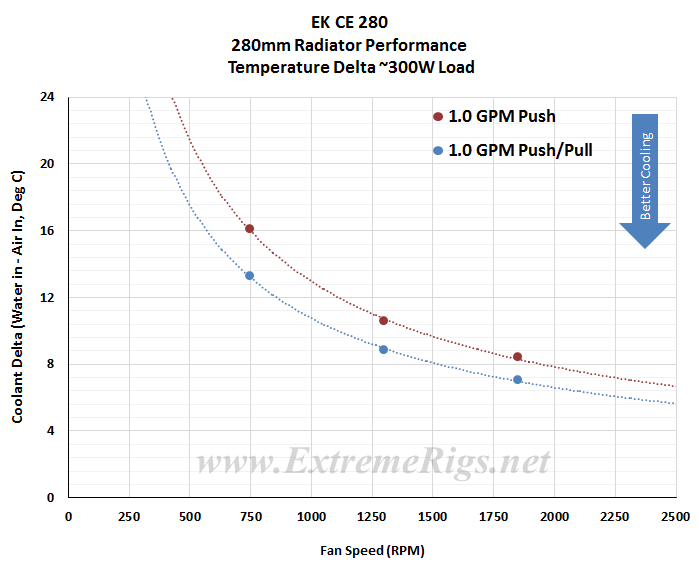
Delta T results (as above) are not always helpful when thinking about how many radiators you would need to cool your system. Instead it’s more useful to know the metric of W/Delta C. This metric is plotted below. It tells us how many Watts are dissipated by the radiator when the coolant rises 10C above ambient temperatures. (W/10 Delta T):
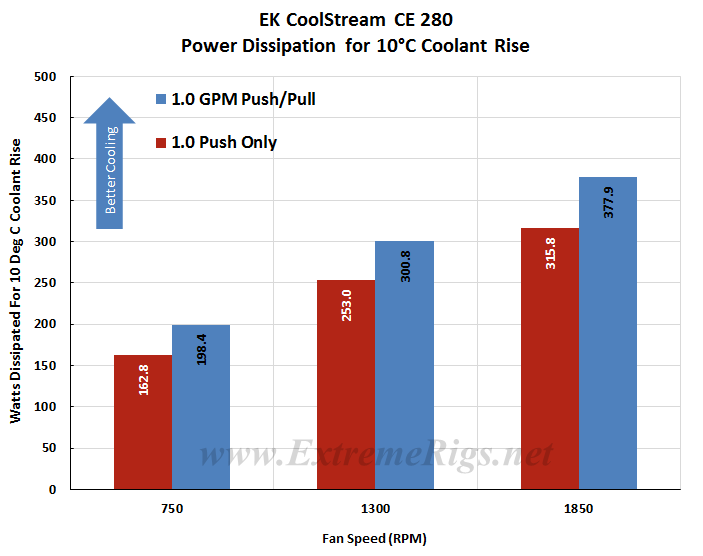The average difference between Push Only and Push/Pull results at the same fan speed was ~17% which is the 2nd highest average of the test group of the test group and indicates that we should see a bias towards either low or high fan speeds. Variance ranged from ~18% at 750 rpm to 16% at 1850 rpm. This very close percentage difference shows that the CE 280’s potential performance scales evenly across different fan assemblies as the fan speeds were increased.
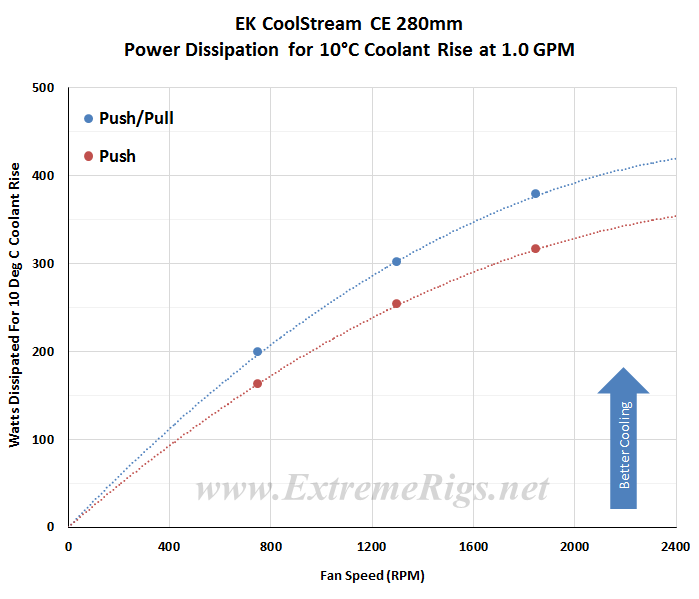
This same data can now be plotted on a chart so that an end user can interpolate their own fan speed. Note again that the extrapolation of the curve is much more sensitive to error than in between the tested range.
Now let’s analyze that data some more…
Your dear should specify the results in Celsius, Fahrenheit or Kelvin throughout your test. Because a conversion from Watts to the indicated temperatures is very inaccurate.
There is no formula with which you can convert from Watts in Celsius, Fahrenheit, or Kelvin, therefore your information is not meaningful and belong in a storybook
If you give me even a chemical or physics book shows where the formula is there, you would win the Nobel Prize. Other websites have soagr refuted your moronic calculation.
Thanks Steffen for your well researched and objective comment. All the plots are clearly labelled “Deg C” meaning degrees, celsius. So I’m not sure if you actually read the article or if you’re another keyboard jockey who wants to shit over other’s hard work because you have nothing better to do? As for our “moronic” calculation. Yes actually there is a calculation to generate power dissipation from temperature change within a liquid. If you know your flow rate, as we do, then you can use the specific heat capacity of the volume of water in question (the coolant in question) combined with the temperature change of the water to generate the energy cooled/second. Energy/Time is also know as Power (at least for steady state equilibrium as this is). So yes thank you for the offer but there is no need to award us a nobel prize for such basic physics, but maybe a bit of humble pie for you would be in order? Maybe even cite your sources next time as to why our calculation is so “moronic”?
Well, I found your reviews VERY helpful; in fact, I’m basing my purchase from info in your reviews…I need a dual fan (push only) radiator that’s 50 mm thin or thinner, that’s readily available (price don’t too much matter)…based on your reviews, and the needs listed above, I have decided on this EK Coolstream 280 CE (with the Alphacool XT45 coming in a close 2nd). I don’t have fans for it yet, because that’s depending on the rad being purchased (this rad is just being used as a secondary rad to the main Aquacomputer 480 rad I have).
Comments are closed.