The Thermal Data
Moving on from the restriction test bench the Nemesis GTX radiator was loaded into the thermal test chamber for a series of 9 tests – consisting of 3 flow rates, each having 3 different fan rpm rates tested. I felt the thermal test data was most important and which you as the reader would be most interested in.
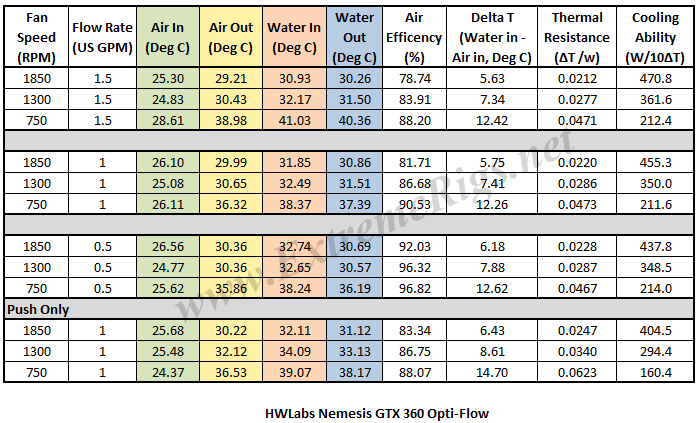
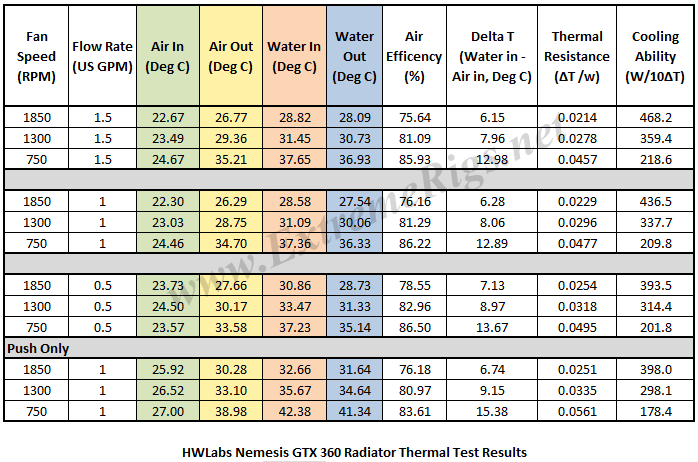
Below is the final data results gathered from at least 2 data logging runs at each flow rate and fan rpm combination. The most stable 15 minute period from each logging run was used and then averaged with the other runs to obtain the data for the table below. A total of 16 temperature sensors were used in the thermal test chamber (8 air in, 2 air out, 3 water in, 3 water out) each take a reading every second and logged via a CrystalFontz unit. The data in the table below is the result of the logging runs which has then been used to create all the plots and tables there-after.
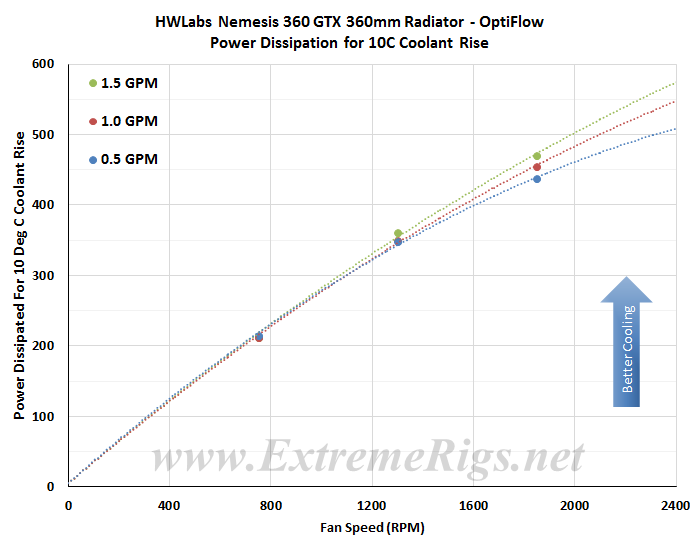
The performance metric of critical importance is the delta between the warm coolant temperature in and the cold ambient air temperature in to the radiator. Given that the system is well insulated and in equilibrium and we know the heat input to the system then we can also calculate a very important number – that is the amount of power required to raise the coolant temperature 1C (or 10C which is more useful reference point). First – the better “optiflow” results:
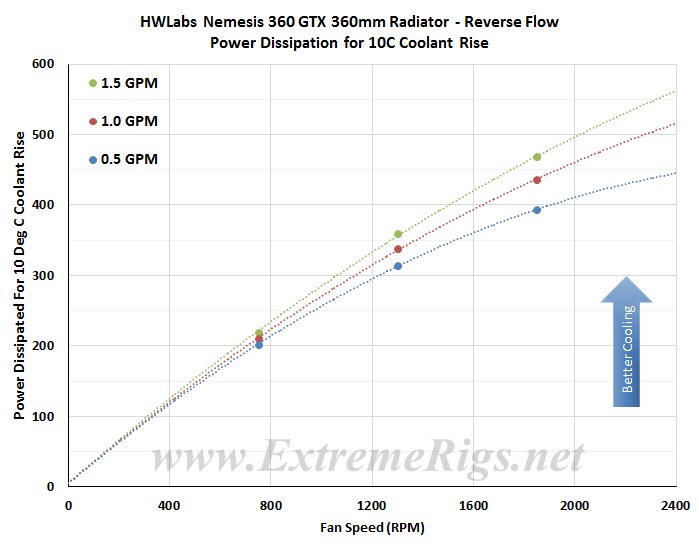
Now for the “reverse” flow:
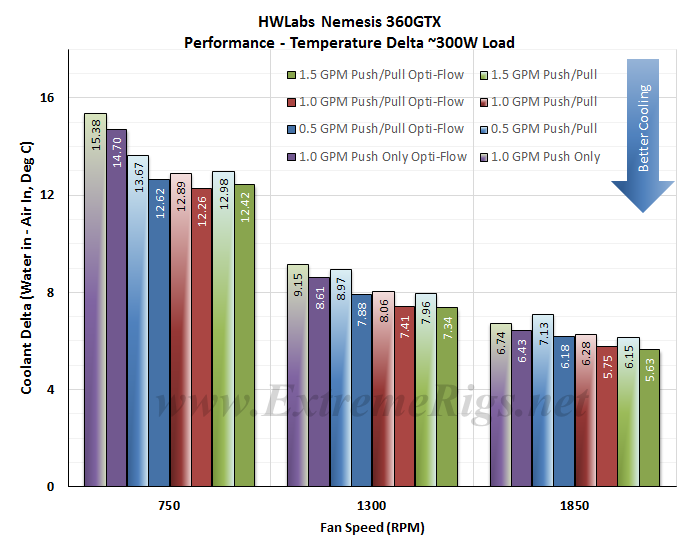
Like the vast majority of the other radiators tested, the Nemesis GTX cares little about flow rate, particularly above 1.0GPM. Here are some plots to show the variance:
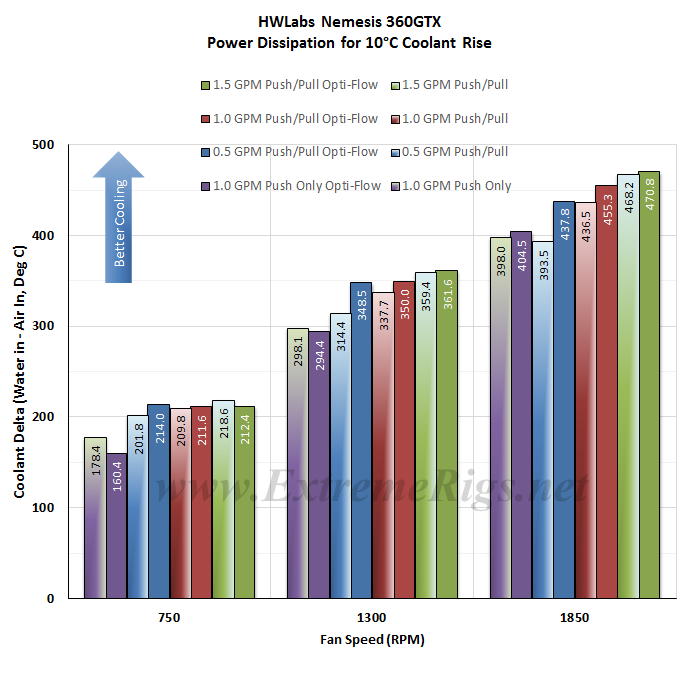
When combining all this data it gets confusing very quickly. The Delta T is not always helpful when thinking about how many radiators you would need to cool your system, nor does it factor in any power variation due to the flow rate/pump changes. Instead it’s more useful to know the delta/W, or more usefully, the inverse metric of W/delta C.
The metric plotted below tells us how many watts are dissipated by the radiator when the coolant rises 10C above ambient temperatures. (10 Delta T):
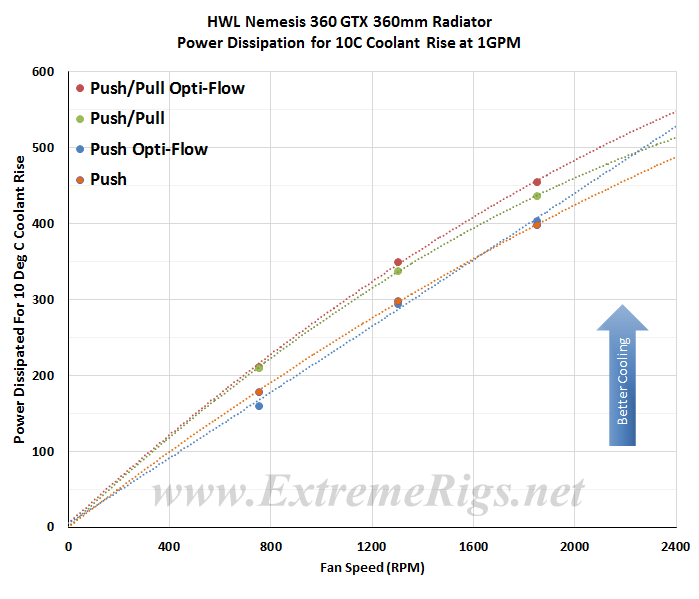
As expected increasing fan speed and therefore airflow through the radiator is the primary determinant in changing the radiators performance. This data can now be plotted as a pretty curve so that an end user can interpolate their own fan speed. Note again that the extrapolation of the curve is much more sensitive to error than in between the tested range. Let’s also separate out the data – first up opti-flow push/pull:
This is the most tightly matched set of data with respect to flow rate variation. The curves only really seperate a little at 1850RPM. Compare to the “reverse” flow:
“OptiFlow” therefore makes a huge difference for cases when flow rate is lower. However when flow rate is high enough, “optiflow” or “reverse” doesn’t make a difference.
This makes it easier to see that at higher fan speeds that a low flow starts to impact the cooling performance. This makes sense if you take it to the extreme and think about a very low flow rate where the coolant is already cooled 99% of the way to ambient with 10% of its journey through the radiator. In this example the radiator is not being efficiently used. 90% of the radiator surface area would then be wasted and you could have used a smaller radiator.
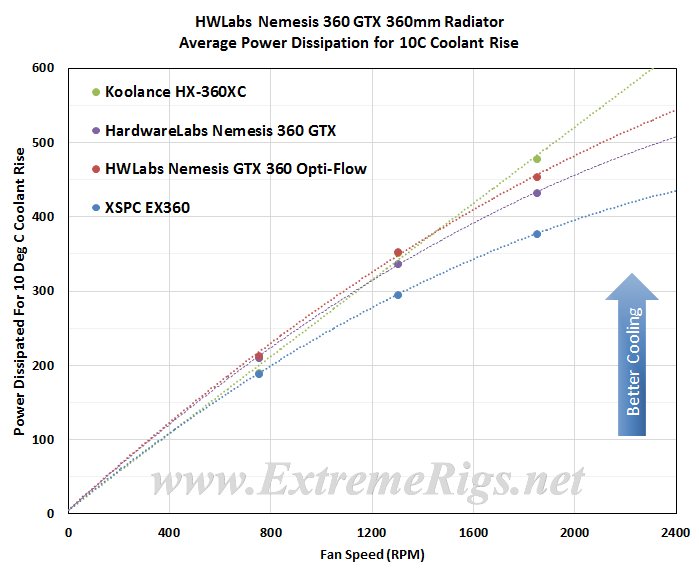
Having said all of this in this next plot all three flow rate results were averaged together to produce one curve. This works well because the radiator was so flow rate insensitive. Averaging reduces test error of course so this helps further to be sure of our data and is more useful therefore for comparing to other radiators.
Finally let’s also compare push to push/pull:
The data for push/pull looks much better. Push only data (particularly at 750RPM) was always a little funky with measured power running low for some reason. This could have been due to the setup. OptiFlow required more fittings and tube in order to mount it in the test chamber. When seen in this plot though, the differences look small.
Now let’s analyze that data.













[…] III 360 Radiator Hardware Labs Black Ice GTX 360 Radiator Hardware Labs Nemesis GTS 360 Radiator Hardware Labs Nemesis GTX 360 Radiator Hardware Labs SR-1 360 Radiator Hardware Labs SR2 360 Radiator Koolance HX-360XC 360 Radiator […]
When compared with the Nemesis GTS radiators, the Nemesis GTX radiators have the same 16 FPI (slightly less in this case), with essentially twice the core thickness and tubing length. Therefore it doesn’t make any sense that they would perform worse than the GTS at 750 RPM in the push only test.
It also doesn’t make sense that the GTS X-Flow performs significantly lower than the standard GTS at 750 rpm. Xflow radiators do perform slightly worse than their Uflow counterparts but not to this extent.
Nemesis 360 GTX Opti-Flow Push@750 rpm – W/10DeltaT= 160.4
Nemesis 360 GTS Xflow Push @750 rpm – W/10DeltaT = 161.1
Nemesis 360 GTS Push @750 rpm – W/10DeltaT= 191.5
So what is happening here?
I’ve noticed that there are no wattage values provided and no mention of how you’ve calculated heat resistance. On the graphs you’ve blanketed the results under a “~300W load” label. The lack of wattage results along with the vague “~300W load” label suggests to me that the power of your heater isn’t being kept constant.
Note: I do not know how you’ve calculated thermal resistance but I presume that you’ve averaged power data over time and used that value (please correct me if I’m wrong).
Working backwards from your results, I’ve calculated some of the wattage values.
The wattage of your heat source can be calculated by dividing Delta T by thermal resistance.
360 Nemesis GTX Opti-Flow results
Push@750 rpm
Delta T – 14.70
Delta T/W – 0.0623
W = 14.70 / 0.0623 = 235.95 W
@1300 rpm
Delta T – 8.61
Delta T/W – 0.0340
W = 8.61 / 0.0340 = 253.23 W
@1850 rpm
Delta T – 6.43
Delta T/W – 0.0247
W = 6.43 / 0.0247 – 260.32 W
From these results it is apparent that the wattage from your heat source varies and therefore so must the heat output.
Have a look at the 750 rpm reverse flow results.
Push@750 rpm = 15.38 / 0.05261 = 274.15 W
Push@1300 rpm = 9.15 / 0.0335 = 273.13 W
Push@1850 rpm = 6.74 / 0.0251 = 268.52 W
You can see that wattages are higher for this set of results and thus more heat is being input to the system by the heater. Therefore the results for W/10DeltaT are now higher than they should be relative to the Opti-Flow results.
Because of this, we cannot directly compare the two data sets unless we make the heat load constant for both sets of results.
Now how does this relate to the 360 GTS and 360 Xflow radiators? Do they experience the same heat load in these tests?
Nemesis 360 GTS Push @750 rpm = 14.62 / 0.0522 = 280.07 W
Nemesis 360 GTS Xflow Push @750 rpm = 15.31 / 0.0621 = 241.54 W
Nemesis 360 GTX Opti-Flow Push @750 rpm = 14.70 / 0.0623 = 235.95 W
The answer is no, and here in lies the problem with most of these results.
Comparing a radiator dissipating a 280W load to a radiator dissipating a 235W and 241W load is not a fair comparison as one has more heat available to dissipate than the others.
There is a 44W difference between the GTS and the GTX radiator. By comparison there is 39W difference between the GTS and the Xflow radiator.
This shows that the GTS radiator is being subjected to significantly more heat than both the GTX and Xflow radiators which explains why the dissipation is higher.
So how do we compare them? How much does the 360 GTX and 360 Xflow actually dissipate at 280W?
Since there are no data points for the GTX radiator at this wattage, we have to extrapolate from the current data points.
First we work out how much more of a heat load the GTS radiator experiences.
Relative to the 360 GTX – 280.07 / 235.95 = 1.187
Relative the 360 Xflow – 280.07 / 241.54 = 1.159
The GTS has a 1.187x (18.7%) higher heat load available to dissipate than the GTX.
The GTS has a 1.159x (15.9%) higher heat load available to dissipate than the Xflow.
Then by using the W/10DeltaT for these radiators at 750 rpm and multiplying it by the above values respectively, we can make the effective load the same for all three radiators. This should give us a better idea of how much each radiator is actually dissipating.
Nemesis 360 GTX Opti-Flow Push @750 rpm (235W load) – W/10DeltaT = 160.4
Nemesis 360 GTX Opti-Flow Push @750 rpm (estimated 280W load) – 1.187 x 160.4 = 190.4
Nemesis 360 GTS Xflow Push @750 rpm (241W load) – W/10DeltaT = 161.1
Nemesis 360 GTS Xflow Push @750 rpm (estimated 280W load) – 1.159 x 161.1 = 186.7
Nemesis 360 GTS Push @750 rpm (280W load) – W/10DeltaT = 191.5
We’ll also have a look at the reverse flow result at this rpm.
Nemesis 360 GTX Reverse Flow Push (274W load) @750 rpm W/10DeltaT= 178.4
Nemesis 360 GTX Reverse Flow Push @750 rpm = 15.38 / 0.0561 = 274.15
280.07 / 274.15 = 1.021 (2.1%)
Here, the GTS has a 1.021x (2.1%) higher heat load available to dissipate than the GTX.
Nemesis 360 GTX Reverse Flow Push @750 rpm (280W load) – 274.15 x 1.021 = 182.1
Comparing the results in this manner does assume that the rate of heat absorption remains the same under the higher load (though it will likely differ slightly). That said the numbers do give a better overall idea to the actual performance of the radiators.
As we can see there is now next to no difference between the watts dissipated per 10 degree delta, when comparing the GTX Opti-Flow and the standard GTS radiator.
We also see that the GTX Opti-Flow result outperforms the reverse flow result by ~9W dissipated.
The GTS Xflow result is now much closer to the standard GTS result only differing ~5W dissipated and this lines up exactly with how Xflow radiators perform relative to Uflow radiators.
But is this just all just a coincidence? After all these are extrapolations. These values were not measured at those wattages but instead were calculated estimates based on those measurements. And they are all showing me exactly what I wanted to see (logical sense).
In my opinion, its far more accurate to draw conclusions when you make these extrapolations than simply drawing conclusions from the results as they are presented currently.
I’ll compare the 280 GTX, GTS and Xflow radiators to these ones sometime in the next few days and we’ll see whether or not my method holds up. But in the mean time, feel free to depict anything incorrect with what I’ve said and I’ll be glad to discuss it.
Ok so first off – if we were to start this thing all over we would be doing it slightly differently as we learned things along the way. We still think we have the most accurate data out there simply because one of the things we learned was how hard it is to test radiators well. Now if it wasn’t going to take 18 months to retest everything we already would have started over.
So I’m not going to address everything in your post at this time because I think we need to start off with the same fundamentals of what the test is otherwise we can go around in circles with math.
So you mentioned the heater. The heater is a 300W aquarium heater totally immersed into a reservoir. The voltage was adjusted with a variac so that it was nominally using 300W in every test.
However because we change flow rates and pump power then there are a few more variables than we would like. Changing pump power adds more heat to the loop. Changing the flow changes the heat loss from the loop. Not all of the heat from the heater gets cooled by the radiator as some of it is passively dissipated. To fight this we insulate the tubes, but insulation isn’t perfect (particularly at higher temperature deltas) and there are various things which can’t be insulated like the flow mete.
SO after we realized just how large an effect this was we switched from simply measuring the deltas to compute the cooling to also having to also measure the power dissipation of the radiator every test. So yes purely looking at deltas in our test isn’t an apples to apples comparison. That is why we compute the W/DT because that is more apples to apples and we believe is a fair enough comparison. I think a better setup would be to keep the pump power fixed and allow flow to vary – this reduces any power contribution from the pump but the flow still varies slightly so passive heat loss still changes. I would also then switch to a less accurate flow rate sensor that can be insulated. However I think the large variation in delta T from varying fan speed also changes the passive cooling effect considerably because the insulation isn’t perfect. In our 750RPM tests, the coolant was often 15-20C over ambient which we would consider too high for a normal PC system. That cooling actually helps worse radiators to perform a little better because the warmer the coolant the more the benefit of passive cooling. I think a fairer comparison is to actually keep the Delta T constant at 10C and vary the heater power accordingly. However this still requires measuring the power dissipated by the system which is what really introduces error to the measurements and means we have to take weeks to take data on a single radiator. The power dissipation of the radiator is based off the coolant delta across the radiator which will often be ~1C, so to get a <1% error you're looking at measuring to an accuracy of <0.01C which is incredibly hard with the kinda of temperature probes we can afford.
So does this answer the questions on how we tested these radiators? If so then we can move on to the results themselves
Comments are closed.